|
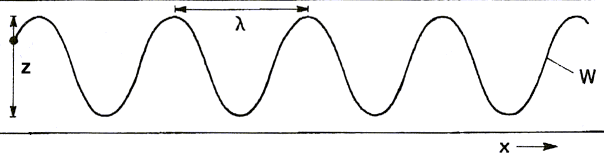
z: Vibration du stylet d'une amplitude ±A0 λ: Longueur de l'onde x: Déplacement de la bande à la vitesse c w: Onde résultante Figure 1a: Vibration d'un stylet sur une bande en déplacement |
![[Photo de l'auteur]](../../common/images/John-Perr.gif)
original in fr John Perr
Utilisateur Linux depuis 1994; il est un des éditeurs français de la revue LinuxFocus. Ingénieur Mécanicien, MSc Sound and Vibration Studies
*pour musiciens et informaticiens.
Si vous avez toujours eu
envie de réaliser vos propres enregistrements ou bien de triturer le son
dans tous les sens avec votre ordinateur, cet article est fait pour vous.
![[Illustration]](../../common/images/article271/illustration271.png)
Cet article se veut pédagogique et espère fournir au lecteur une base nécessaire à la
compréhension générale du son, sa manipulation et son interprétation. Bien sûr, la musique est
concernée au premier chef mais elle n'est qu'un bruit parmi d'autres souvent moins agréables.
Ainsi, nous abordons dans un premier temps, les concepts physiques de base qui régissent
le son, sa propagation et son interprétation par l'oreille humaine. Nous nous intéresserons
ensuite au notions de signaux, c'est à dire à ce que devient le son quand il est enregistré
et en particulier avec les systèmes numériques récents comme les échantillonneurs
(anglicisme samplers) et les ordinateurs.
Enfin nous aborderons les systèmes de compression à la mode comme le mp3 ou Ogg Vorbis.
Les sujets abordés ici se veulent accessibles à tous et l'auteur a essayé d'utiliser des termes
courants et en particulier ceux connus des musiciens. Quelques formules apparaissent ici ou là
dans les illustrations mais ne sont absolument pas nécessaires à la compréhension (ouf).
Si l'on ne s'intéresse qu'au phénomène physique, le son est la vibration mécanique d'un support
gazeux, liquide ou solide. C'est l'élasticité de ce milieu qui permet au son de rayonner depuis
la source sous formes d'ondes, exactement comme les ronds que produit un caillou lancé dans l'eau.
Chaque fois qu'un objet vibre, une petite proportion de son énergie est perdue dans le milieu
environnant sous forme de sons. Levons tout de suite un doute: le son ne se propage pas dans le vide.
La figure 1a montre comment un stylet attaché à une source de vibration,
comme un haut-parleur par exemple, se transforme en onde, quand on fait défiler une bande de
papier devant sa pointe.

|
z: Vibration du stylet d'une amplitude ±A0 λ: Longueur de l'onde x: Déplacement de la bande à la vitesse c w: Onde résultante Figure 1a: Vibration d'un stylet sur une bande en déplacement |
Dans le cas de l'air, le son se propage sous forme d'une variation de pression que lui
communique par exemple un haut-parleur. La compression (faible) se propage dans l'air.
Notez que seule la compression se déplace et non l'air. Dans le cas des ronds dans l'eau, cités
au-dessus, les vagues se déplacent, mais l'eau reste au même endroit, elle ne fait que se
déplacer de haut en bas et non suivre les vagues. Un bouchon placé sur l'eau reste à la même
position sans se déplacer. Pour cette raison, il n'y a pas de "vent" devant un haut-parleur,
les ondes sonores se déplacent à environ 344 mètres par secondes dans de l'air à 20°C, mais
les particules d'air ne bougent que de quelques microns.
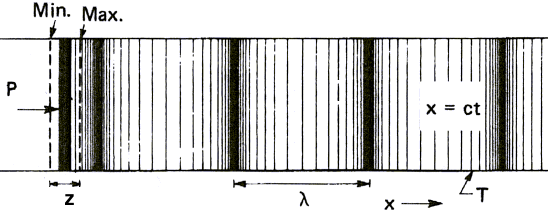
Nous avons vu sur les dessins ci-dessus que les ondes prennent des formes de vagues. La distance
entre deux crêtes est appelée longueur d'onde et le nombre de crêtes que voit
passer un observateur pendant une seconde est appelé fréquence. Ce terme utilisé en physique
n'est rien d'autre que la hauteur d'un son pour des musiciens. Une fréquence faible correspond à
un son grave, une fréquence élevée à un son aigu.
La figure 2 donne des valeurs pour ces deux grandeurs et pour un son se propageant
dans l'air:

Une autre caractéristique importante d'un son est son amplitude. Il peut être fort ou doux. Dans l'air cela correspond à des variations de pressions grandes ou petites selon que l'air est fortement comprimé ou non. En acoustique, la force d'un son se mesure en décibel. C'est une unité un peu compliquée mathématiquement, comme le montrent les figures 3a et 3b. Elle a été choisie ainsi parce que cela permet d'avoir des chiffres aisément manipulables et parce que nous verrons au chapitre suivant que cette formule logarithmique correspond à ce que perçoit l'oreille humaine. C'est malheureux à dire mais vous faites des maths sans le savoir:
| Figure 3a: Niveau de bruit en pression | Figure 3b: Niveau de bruit en puissance |
Pour l'instant, il nous suffit de retenir que les dB expriment la puissance acoustique d'un son
et que 0 dB correspond au minima que l'oreille humaine peut percevoir et non à l'absence de sons.
Les décibels représentent en effet une mesure relative du bruit par rapport à ce que peut entendre
un humain. Il suffit de changer la référence (Po ou Wo ci-dessus) pour que la valeur soit complètement
différente. C'est pourquoi les dB gradués sur le bouton de volume de votre chaîne Hi-fi ne correspondent
pas du tout à des niveaux acoustiques mais à des puissances électriques de sortie de l'amplificateur,
ce qui n'a quasiment rien à voir, le 0 db représentant bien souvent la puissance maximale que
l'amplificateur est capable de délivrer. Acoustiquement parlant le niveau en dB est bien
supérieur, sinon vous n'auriez pas acheté cet amplificateur-là, mais cela dépend aussi de vos enceintes...
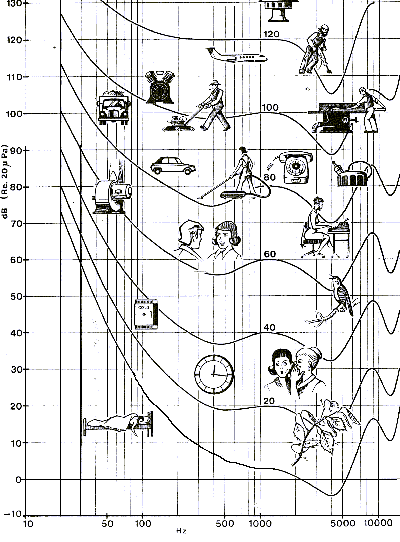
La figure 4 situe quelques sources courantes de bruit en amplitude et en fréquence. Les courbes
montrent les niveaux perçus comme égaux par l'oreille humaine; nous y reviendrons plus bas:
Par comparaison, et pour fixer les idées, le tableau ci-dessous reprend les niveaux en décibels et en watt de quelques sources courantes de bruit. On notera que la notation en décibel permet de manipuler plus facilement les chiffres:
| Puissance (Watt) | Niveau dB | Exemple | Puissance (W) |
|---|---|---|---|
| 100 000 000 | 200 | Fusée Saturn V Gros porteur quadriréacteurs |
50 000 000 50 000 |
| 1 000 000 | 180 | ||
| 10 000 | 160 | ||
| 100 | 140 | Grand orchestre | 10 |
| 1 | 120 | Marteau piqueur | 1 |
| 0.01 | 100 | Cri | 0.001 |
| 0.000 1 | 80 | ||
| 0.000 001 | 60 | Conversation | 20x10-6 |
| 0.000 000 01 | 40 | ||
| 0.000 000 000 1 | 20 | Chuchotement | 10-9 |
| 0.000 000 000 001 | 0 | ||
| Puissances acoustiques de sources courantes de bruit | |||
Il existe plusieurs façons de mesurer l'amplitude d'un son, et par extension, d'un signal quelconque de nature ondulatoire. La figure 5 illustre cela:
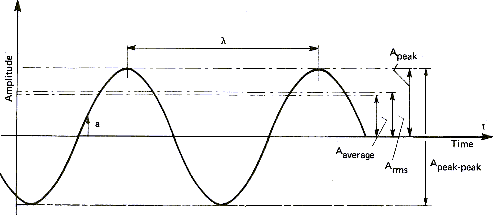
| Repère | Dénomination | Définition | ||||||
|---|---|---|---|---|---|---|---|---|
| Aaverage | Amplitude moyenne | Valeur moyenne arithmétique du signal positif | ||||||
| ARMS | Amplitude efficace | Amplitude continue équivalente en puissance | ||||||
| Apeak | Amplitude crête | Amplitude maximale positive | ||||||
| Apeak-peak | Amplitude crête à crête | Amplitude maximale positive et négative | ||||||
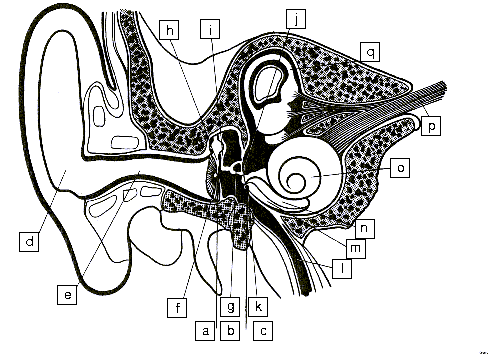 |
a) Oreille externe b) Oreille moyenne c) Oreille interne d) Pavillon e) Conduit auditif f) Tympan g) Etrier h) Marteau i) Enclume j) Fenêtre ovale k) Fenêtre ronde l) Trompe d'eustache m) Scala Tympani n) Scala vestibuli o) Cochlée p) Fibre nerveuse q) Canaux semi-circulaires |
|
| Figure 12: Principales parties de l'oreille | ||
Les mouvements de l'étrier sont transmis, via la fenêtre ovale et le vestibule, au limaçon aussi appelé cochlée. Le limaçon contient deux chambres séparées par la membrane basilaire, elle-même recouverte des cellules cillées sensibles aux vibrations et reliées au nerf auditif (Voir les figure 13 et 14 ci-dessous). La membrane basilaire agit comme un filtre spatial. Ainsi les portions du limaçon ont différentes sensibilités selon les fréquences ce qui permet au cerveau de différencier la hauteur des sons.
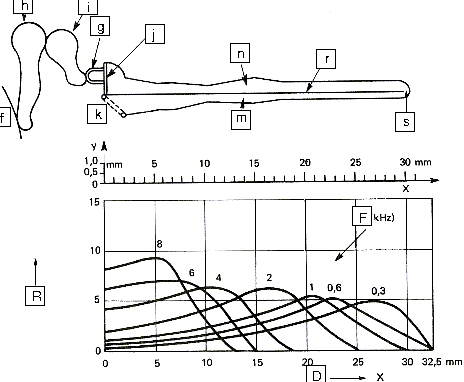 |
f) Tympan g) Etrier h) Marteau i) Enclume j) Fenêtre ovale k) Fenêtre ronde m) Scala Tympani n) Scala vestibuli r) Membrane basilaire s) Helicotrema R) Réponse relative F) Réponse en Fréquence D) Coordonnée sur la membrane |
|
| Figure 13: Section de la cochlée | ||
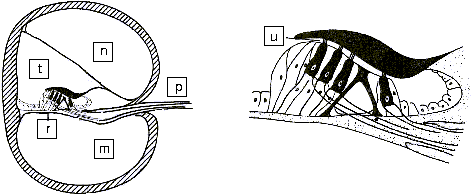 |
m) Scala Tympani n) Scala vestibuli p) nerf auditif r) Membrane basilaire t) Scala media u) Cellules ciliées |
|
| Figure 14: Section transversale de la cochlée | ||
Le rôle du cerveau est particulièrement important car il fourni un gros travail
d'analyse pour reconnaître les sons, selon leur hauteur bien sûr, mais aussi selon
leur évolution au cours du temps. Le cerveau permet aussi la corrélation entre
les deux oreilles afin de situer le son dans l'espace. C'est lui qui nous permet
de reconnaître un instrument ou une personne précise et de les situer dans l'espace.
Il semble qu'une grande partie du travail effectué par le cerveau soit apprise.
La figure 15 montre comment nous percevons l'intensité des sons en fonction des
fréquences.
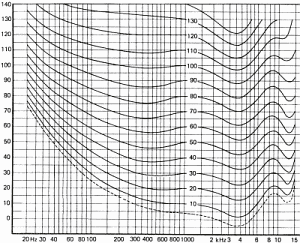
Les courbes ci-dessus ont été tracées pour une population moyenne. Il existe de grandes disparités entre les individus et plusieurs facteurs influencent directement l'audition:
La figure 16 montre l'influence de l'age sur la perte d'audition à différentes fréquences. Selon les sources citées, les résultats sont différents. Cela s'explique aisément par le fait que de grandes variations sont observées dans la population et que ces études ont du mal à ne prendre en compte que l'âge des individus. Il n'est pas rare de voir des musiciens âgés avec des oreilles de jeune homme, tout comme il existe des jeunes avec des oreilles prématurément dégradées par des expositions répétées à des sons trop forts tels que ceux des concerts ou de boîtes de nuits.
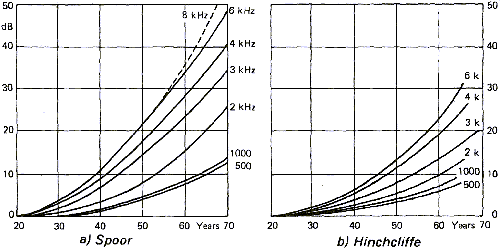
Les pertes d'audition dues au bruit dépendent à la fois de la durée d'exposition
et de l'intensité du bruit. Remarquez que l'on désigne ici tous les sons comme du "bruit"
et pas seulement ceux qui sont désagréables. Ainsi, écouter à fond de la musique au casque
ou bien regarder les avions décoller de l'aéroport a exactement le même effet sur
les cellules auditives.
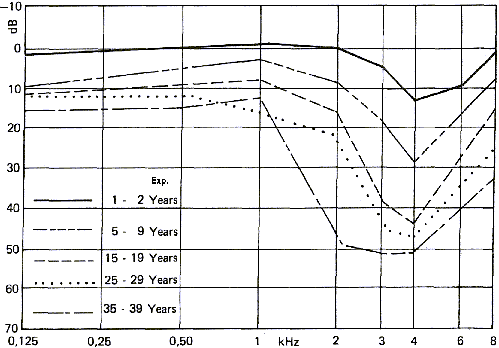
La figure 17 montre l'effet sur l'audition de l'exposition au bruit. Notez
que les effets sont différents de ceux de l'âge. Avec l'âge, l'oreille devient
moins sensible aux hautes fréquences alors que l'exposition au bruit diminue nettement
la sensibilité autour de 3-4 Khz, fréquence où l'oreille est la plus sensible d'habitude.
Ce type de perte d'audition se rencontre très fréquemment chez les utilisateurs
d'armes à feu.
Reportez-vous au chapitre sur le calcul des décibels. Vous remarquerez que
plusieurs dizaines de décibels représentent des écarts très importants de pression
acoustique. En fait, graduer une échelle linéaire en décibels revient à en
tracer une logarithmique en pression. Ceci est dû au fait que l'oreille et
le cerveau sont adaptés à ces très grandes variations tant en amplitude
qu'en fréquence. La plus haute fréquence audible par l'oreille humaine est
mille fois supérieure à la plus basse et le son le plus fort peut être
un milliard de fois plus fort que le plus faible audible (un rapport d'intensité
de 1012 à 1).
Ainsi, le calcul montre qu'un doublement de pression représente 3 dB. Pour l'oreille
cette variation est perceptible mais il faut une augmentation de 9 dB de l'intensité
acoustique pour que l'être humain ait l'impression d'un doublement de la force
du son. Cela représente en fait une pression acoustique 8 fois plus forte!
En fréquence, c'est le changement d'octave qui correspond à un doublement de
fréquence. Là aussi nous percevons donc linéairement l'évolution logarithmique
d'un phénomène physique.
Ne sortez pas tout de suite votre calculatrice, nous verrons plus bas comment
calculer les hauteurs des notes de la gamme.
Enregistrer un son sur un système analogique comme une bande magnétique ou un disque en vinyle est encore une opération courante même si elle tend à être détrônée par les moyens numériques. Dans les deux cas, transformer une onde sonore en variations magnétiques ou en données informatiques, introduit des limitations dues justement aux moyens d'enregistrement. Nous avons déjà parlé rapidement des effets de l'échantillonnage sur le spectre d'un son. Étudions maintenant les autres facteurs qui transforment les sons lorsqu'ils sont enregistrés.
La "dynamique" d'un système d'enregistrement est le terme utilisé pour désigner
la différence qui existe entre les amplitudes minimum et maximum que le dit système
peut enregistrer. Cela commence généralement par le microphone, qui convertit
le son en signal électrique, pour aller jusqu'au support de l'enregistrement, disque,
bande magnétique ordinateur...
Rappelez-vous que les décibels expriment un ratio. Dans le cas de la dynamique, la
valeur donnée correspond au maximum pour un minimum qui vaut 0dB.
Voici quelques exemples:
Un orchestre symphonique peut jouer des sons sur une gamme allant jusqu' à 110 dB. Pour cette raison, les fabricants de disques utilisent des systèmes qui compriment la dynamique afin d'éviter que les signaux forts ne soient écrêtés et les faibles inaudibles.
En plus d'être moins performants que l'oreille humaine, les systèmes d'enregistrement ont aussi le défaut d'émettre leur propre bruit. Cela peut être le frottement de la tête de lecture sur le disque vinyle ou le ronflement de l'amplificateur. Ce bruit, généralement assez faible limite la dynamique de l'appareil vers le bas. Il est perçu la plupart du temps comme un ronflement ou un souffle qui s'entend bien avec un casque de bonne qualité. Ce souffle ressemble à un bruit de chute d'eau car il a un spectre assez large composé de nombreuses fréquences.
Les filtres ont un effet important sur la phase d'un spectre car ils introduisent
très souvent un décalage des signaux qui dépend de la fréquence. Ceci conduit à une
déformation appelée distortion harmonique car elle affecte les harmoniques d'un signal.
Tous les appareils et systèmes qui concourent à enregistrer un signal se comportent
comme des filtres et de fait introduisent une distortion du signal. Bien entendu, la
chaîne de restitution des enregistrements ne déroge pas à cette règle et amène
elle aussi son lot de distortions et bruits, depuis les têtes de lectures jusqu'aux
hauts-parleurs en passant par les câbles et connecteurs.
De plus en plus, des algorithmes de compression comme le mp3 ou bien ogg vorbis
sont utilisés pour gagner une précieuse place sur nos supports d'enregistrement.
Ces algorithmes sont dit "destructifs" car ils détruisent une partie du signal sonore
pour gagner un maximum de place. Les programmes de compressions utilisent un modèle
de l'oreille humaine afin d'éliminer les informations inutiles. Par exemple, si deux fréquences
sont proches l'une de l'autre, la plus faible pourra être éliminée si elle est considérée
comme masquée par la plus forte. Pour cette raison, on trouve sur internet un certain
nombre de tests et de recommandations sur la manière d'utiliser ces logiciels pour éviter
une dégradation audible des enregistrements. Il ressort de ceux que l'auteur à consulté
que de nombreux encodeurs mp3 filtrent systématiquement les signaux supérieurs à 16 KHz
et se limitent à un bit rate de 128Kps. Ces chiffres s'avèrent largement
insuffisants dans de nombreux cas si l'on souhaite conserver une qualité
d'écoute proche de celle obtenue avec les CD.
A l'opposé les systèmes de compression de données comme
gzip, bzip2, lha ou zip n'altèrent pas les données mais ont des taux de compression
plus faibles. Il faut de plus, décompresser tout le fichier avant de l'écouter, ce qui
s'accommode assez mal des baladeurs et autres lecteurs.
Afin de fixer les idées voici la comparaison de quelques termes musicaux et scientifiques. Dans la plupart des cas ces comparaisons ont quand même des limites car les termes utilisés par les mélomanes décrivent plus les perceptions de l'oreille humaine que les phénomènes physiques.
Une note de musique est caractérisée entre autre par sa hauteur et cette hauteur peut être assimilée à la fréquence fondamentale de la note. On peut ainsi calculer la fréquence des notes pures avec la formule suivante:
Si l'on prend pour REF le La à 440 Hz de l'octave 4 comme valeur pilier, cela permet de calculer les autres pour les tons de 1 à 12 soit de Do à Si:
| Note | Octave | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Do | 32,70 | 65,41 | 130,8 | 261,6 | 523,3 | 1047 | 2093 | 4186 |
| Do # | 34,65 | 69,30 | 138,6 | 277,2 | 554,4 | 1109 | 2217 | 4435 |
| Ré | 36,71 | 73,42 | 146,8 | 293,7 | 587,3 | 1175 | 2349 | 4699 |
| Mi b | 38,89 | 77,78 | 155,6 | 311,1 | 622,3 | 1245 | 2489 | 4978 |
| Mi | 41,20 | 82,41 | 164,8 | 329,6 | 659,3 | 1319 | 2637 | 5274 |
| Fa | 43,65 | 87,31 | 174,6 | 349,2 | 698,5 | 1397 | 2794 | 5588 |
| Fa # | 46,25 | 92,50 | 185,0 | 370,0 | 740,0 | 1480 | 2960 | 5920 |
| Sol | 49,00 | 98,00 | 196,0 | 392,0 | 784,0 | 1568 | 3136 | 6272 |
| La b | 51,91 | 103,8 | 207,6 | 415,3 | 830,6 | 1661 | 3322 | 6645 |
| La | 55,00 | 110,0 | 220,0 | 440,0 | 880,0 | 1760 | 3520 | 7040 |
| Si b | 58,27 | 116,5 | 233,1 | 466,2 | 932,3 | 1865 | 3729 | 7459 |
| Si | 61,74 | 123,5 | 246,9 | 493,9 | 987,8 | 1976 | 3951 | 7902 |
Les puristes auront remarqué que cette formule ne différencie pas les demi-tons diatoniques
et chromatiques. Ils peuvent toujours refaire les calculs en prenant un coma comme unité
plutôt que le demi-ton...
Ceci dit, assimiler fréquences et notes est loin d'être suffisant pour caractériser
une note jouée par un instrument. Il faut aussi pouvoir prendre en compte si une note
est piquée (pizzicato) ou liée (legato), préciser de quel instrument elle provient, sans
compter tous les effets possibles tels que le glissando, le vibrato, etc...Pour cela
les scientifiques représentent une note par l'évolution de son spectre au cours du
temps. Il est ainsi possible de voir sur ces "sonogrammes", l'évolution de toutes
les harmoniques.
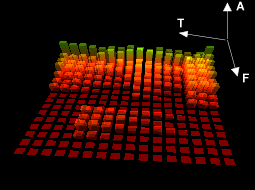
| Figure 18: Exemple de sonogramme | ||
| T: Temps | A: Amplitude | F: Fréquence |
En pratique, la reproduction électronique des sons utilise de nos
jours des appareils entièrement artificiels (synthétiseurs) pour créer des sons de
toutes pièces, ou bien des échantillonneurs (samplers) pour mémoriser un son et le
rejouer à différentes hauteurs avec des effets variés. Il devient ainsi possible
de jouer un concerto pour violon en remplaçant les instruments par des grincements
de chaises pré-enregistrés avec un échantillonneur. Tous le monde peut le faire,
inutile de savoir jouer d'un instrument même si faire grincer une chaise est à la portée
du premier venu...
Ce qui caractérise une note par rapport à une autre est représenté par le schéma ci-dessous:
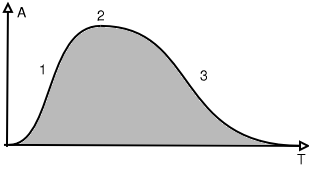
| Figure 19: Caractéristiques d'une note: enveloppe | |
| 1: Attaque | A: Amplitude positive |
| 2: Maintien | T: Temps |
| 3: Chute | |
La courbe représente l'évolution de l'amplitude globale du signal au cours du temps. Ce type de courbe
est appelé courbe enveloppe car elle enveloppe le signal (en grisé sur le dessin). La partie montante constitue l'attaque
et peut être très différente selon le type d'instrument (à vent, à corde, percussion...).
La seconde partie appelée "sustain" en anglais est le corps de la note et constitue souvent
la partie la plus longue de la note à l'exception des notes des instruments à percussion.
La troisième partie est aussi de durée et de forme très variable selon le type d'instrument.
Les instruments permettent aux musiciens d'influer sur ces trois parties. Ainsi, la façon
de frapper les touches d'un piano changera l'attaque de la note alors que les
pédales modifieront
la partie finale (la chute). Chacune des trois parties peut avoir un spectre très différent ce qui
contribue encore à accroître la diversité des sons. Les harmoniques n'évoluent en effet pas ensemble.
Les basses fréquences ont en général tendance à durer plus longtemps que les hautes ce qui fait que
la couleur du son perçue au début de la note n'est pas la même qu'à la fin.
Étant donnée sa définition, la bande passante d'un appareil peut être assimilé à la tessiture d'un instrument. Dans les deux cas on décrit bien l'étendue de fréquences ou de hauteurs dont est capable un instrument. Par contre, la note la plus élevée que peut jouer un instrument correspond seulement à la fréquence fondamentale donnée dans le tableau ci-dessus. En d'autres termes, si l'on souhaite enregistrer un instrument il faut prendre un appareil ayant une bande passante nettement supérieure à la tessiture de cet instrument si l'on souhaite conserver la couleur des notes des octaves supérieures. Une bande passante trop courte filtrera toutes les fréquences harmoniques des notes des octaves supérieures ce qui en dénaturera la sonorité. Dans la pratique, on prendra toujours un appareil ayant au minimum les capacités de l'oreille humaine, soit 20hz à 20Khz, voir plus car la distortion harmonique apparaît bien en deçà de ces valeurs.
En regardant attentivement le tableau des fréquences de notes ci-dessus, les musiciens
vont trouver une correspondance entre les fréquences harmoniques d'une note et celles qui
constituent les accords.
Les harmoniques d'une note sont données par les fréquences multiples de la fondamentale.
Ainsi pour un Do 1 à 32,7 Hz les harmoniques sont:
| Harmonique | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Fréquence | 32,7 | 65,4 | 98,1 | 130,8 | 163.5 | 196,2 | 228,9 | 261,6 |
| Note | Do | Do | Sol | Do | Mi | Sol | Si b | Do |
On retrouve bien les raisons pour lesquelles un accord est parfait (Do-Mi-Sol-Do) ou de 7ième (Do-Mi-Sol-Si b): Les fréquences des notes de l'accord sont en concordance avec celle de la note fondamentale. C'est magique.
Sans entrer dans les détails, nous avons fait un tour d'horizon du son en abordant les aspects physiques, humains et techniques de l'acoustique. Ceci dit, l'appréciation de votre oreille reste quand même le critère ultime de choix. Les chiffres donnés par les mathématiques ou des instruments de mesure sophistiqués peuvent être utiles pour comprendre pourquoi un enregistrement vous semble aussi bizarre, mais ils ne vous diront jamais si les Beatles ont fait de la meilleure musique que les Rolling Stones dans les années 60.
Brüel & Kjaer: Société d'origine Danoise qui fabrique des équipements de mesure de qualité pour l'acoustique et les vibrations. Cette société publie depuis de nombreuses années (une cinquantaine) des ouvrages gratuits et libres d'où sont tirés la majorité des graphiques de cet article. Ces ouvrages sont disponibles au format PDF sous la rubrique Primers.